有关格雷码的一些学习分享
格雷码简介
抄自百度百科,没啥大问题
典型的二进制格雷码(Binary Gray Code)简称格雷码,因1953年公开的弗兰克·格雷(Frank Gray,18870913-19690523)专利“Pulse Code Communication”而得名,当初是为了通信,现在则常用于模拟-数字转换和位置-数字转换中。法国电讯工程师波特(Jean-Maurice-Émile Baudot,18450911-19030328)在1880年曾用过的波特码相当于它的一种变形。1941年George Stibitz设计的一种8元二进制机械计数器正好符合格雷码计数器的计数规律。
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。在数字系统中,常要求代码按一定顺序变化。例如,按自然数递增计数,若采用8421码,则数0111变到1000时四位均要变化,而在实际电路中,4位的变化不可能绝对同时发生,则计数中可能出现短暂的其它代码(1100、1111等)。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。格雷码有多种编码形式。
性质以及构造
格雷码最经典也是最直观的构造方式就是镜像构造,因此,格雷码具有很强的递归性质,在解决一些格雷码的问题时,考虑递归和动态规划有奇效。
镜像构造方法如图(真的很直观):
N位格雷码由N-1位格雷码镜像翻转而来,这种构造方式也揭示了格雷码的循环性质
一位格雷码:
0
——
1
二位格雷码:
0 0
0 1
———
1 1
1 0
三位格雷码:
0 00
0 01
0 11
0 10
————
1 10
1 11
1 01
1 00
第二种就是数学构造(抄自数电老师的教案):
Bit i of a Gray-code code word is 0 if bits i and i+1 of the corresponding binary code word are the same, else bit i is 1.
(when i+1=n , bit n of the binary code word is considered to be 0)
这个性质的基础是格雷码的起始两位 0 1 和二进制码是一致的,因为格雷码是循环码,理论上你可以用任意一个格雷码作为起始位(不过就是没有人会这么做)
int g(int n) { return n ^ (n >> 1); }
同时也可以逆推格雷码转原二进制编码的数学算法:
首先格雷码的最高位肯定和原数二进制位一致,根据构造时的异或规律,反过来可以得到 k 位格雷码的逆变换:
n[k]=g[k];
n[k-1]=g[k-1]^n[k];// 递推
简单化简可知,n 的第 i 位是 g 的 k~i 位的异或:
int rev_g(int g) {
int n = 0;
for (; g; g >>= 1) n ^= g;
return n;
}
多维格雷码
就是每一个维度上都满足格雷码的性质,所以 n 维格雷码就是 n 个格雷码前后拼接的的排列组合
格雷码的镜像递归性质的应用
Q: 现在给你一个 N 个元素的 k 位格雷码数组,规定 M(N) 表示 N 个元素的格雷码数组中元素的最大值,问 M(N) 的所有可能的值的最小值是多少
关于 M(N) 的可能值,当 N 为 2 的幂的时候,M(N) 当然只有一种情况,否者, 根据循环码的性质,格雷码数组有 N 种可能,M(N) < N/2 (至于有多少个多少我以后慢慢想)
格雷码的镜像性质,有没有一种很眼熟的感觉,任意格雷码序列二分,右边一定比左边大,去掉最高位后为降一位的格雷码(完全二叉树既视感)
求最大值中的最小值的思路,最大值由于镜像的平衡二叉树性质,可以肯定和前半段没有关系,并且区间最大值具有重复贡献性,父区间的最大值一定大于等于子区间的最大值,于是得到最优策略是这个数组将前半段(以 0 为前缀)的格雷码全覆盖,观察后半段的所有可能情况,我们发现,问题递归成为了 N-2^(k-1) 个元素的格雷码数组的问题了。
于是
当 N-2(k-1) > 2(k-2) 时,继续递归
当 N-2(k-1) <= 2(k-2) 时,停止递归,此时问题转化为 0~N-2^(k-1) 的格雷码的最大值是多少:
关于 0~X 的格雷码的最大值,根据格雷码的镜像性质,越过二分界限向下递归导致二叉树反转,根据二叉树性质剪枝求最大值,时间复杂度 O(logn) 代码示例如下:
int getMax(int x,int k,bool swap){
if(k==0) return swap?1:0;
int dlvr=1<<(k-1);
if(x<=dlvr) return getMax(x,k-1,swap)+(swap?1<<k:0);
else return getMax(x-dlvr,k-1,!swap)+(swap?0:1<<k);
}
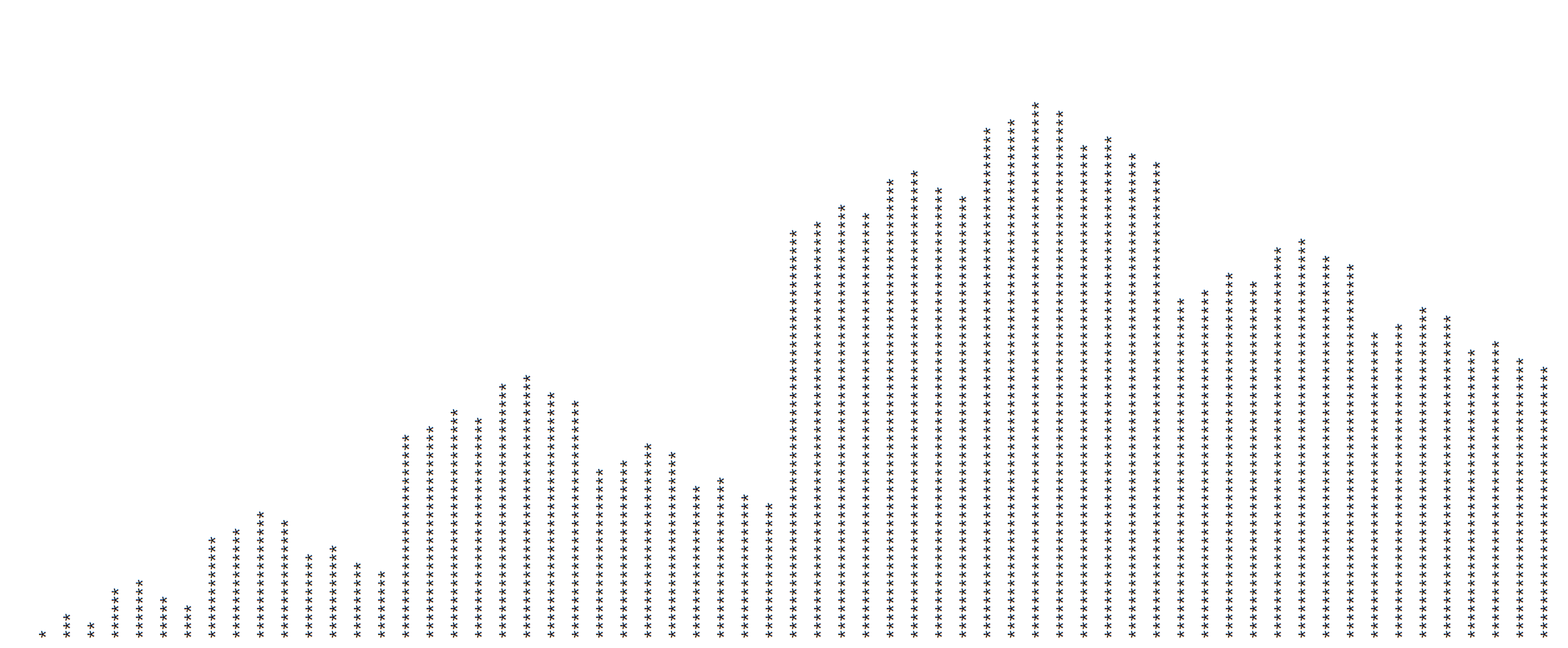
悄悄说一句,代码还没跑过,不代表最终结果,有时间再跑(抄的时候谨慎一点)
格雷码大小性质上类似于完全二叉树。二叉树保证每一层左子树都大于右子树,而格雷码是大的子树反转,小的保持,加上一个 swap 就可以类似完全二叉树(先序遍历生成的数组)那样找最大值。(下面是5位格雷码0~63的大小可视化,某种意义上非常像二叉树)
区间上求最大值的算法,除了格雷码这种特殊规律的,最常用的是 ST表 求最大值,时间复杂度只有 O(1) ,构造比较简单,但时间和空间预处理复杂度 O(NlogN),对于无序静态数组来说是很好的树结构,利用了区间最大值重复贡献的思想,对解决这个问题提供了不少帮助。
最后,感谢一位 IOer 大佬的帮助(滑跪膜拜)
