拉格朗日对偶问题|凸优化
intro:
拉格朗日乘数法求函数的极值和条件极值,是拉格朗日问题的一种简单问题表现。在深度学习的各种优化梯度下降方法中都体现了拉格朗日对偶的思想。
参考视频 https://www.bilibili.com/video/BV1HP4y1Y79e
简要形式:
min\ \ f_0(x), x \in \mathbb{R}^n
\\
s.t.\begin{cases}
f_i(x)\leq0,\ i=1,2,3,...,m \\
h_i(x)=0,\ i=1,2,3,...,q
\end{cases}
\\
L(x,\lambda,\upsilon)=f_0(x)+\sum \lambda_if_i(x)+\sum\nu_ih_i(x)
数学上已经严谨证明,拉格朗日函数求得的最值是原目标函数在约束条件下的最值。
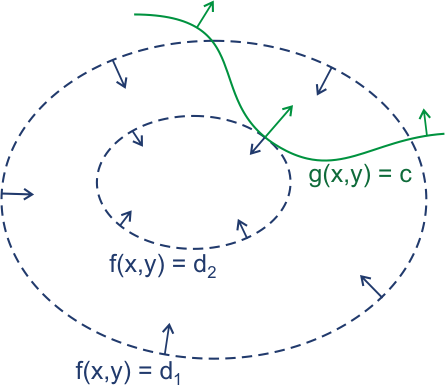
梯度
以简单的拉格朗日乘数法为例
min\ f_0(x,y)\ when\ y\leq g(x)
\\
L(x,y)=f(x,y)+\lambda(y-g(x))
\\
\nabla L(x,y)=0
\\
\begin{cases}
\frac{\partial f(x,y)}{\partial x}+\lambda\frac{\partial (y-g(x))}{\partial x} = 0 \\
\frac{\partial f(x,y)}{\partial y}+\lambda\frac{\partial (y-g(x))}{\partial y} = 0
\end{cases}
可以视为,目标函数和约束条件的梯度矢量在拉格朗日乘子的调节下大小相等,方向相反,此时认为找到最小值点。
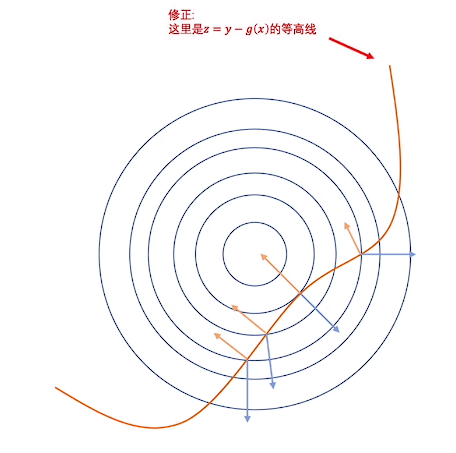
当约束条件复杂时(图中简单表示为二维平面和线性约束条件便于理解,实际上和高维度超平面和非线性约束条件的理解可以互通)
L(x,\lambda)=f(x)+\sum\lambda_ig_i(x) \\
\nabla L(x,\lambda) = 0 \\
-\nabla f(\lambda) = \sum\lambda_i\cdot\nabla g_i(x) \\
依旧解释为,调节拉格朗日乘子(此时要求拉格朗日乘子非负)使得约束条件的梯度的线性组合与目标函数的梯度大小相等,方向相反
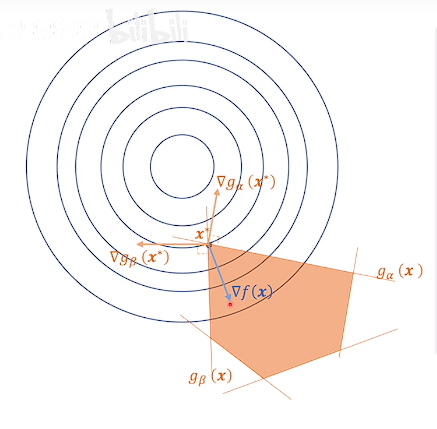
其中一部分约束条件前的拉格朗日乘子系数为0,失去作用(松弛约束条件),没有失去作用的梯度的拉格朗日乘子系数大于0(紧致约束条件)。
全松弛条件:
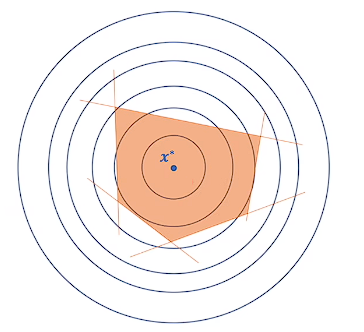
凸问题

实际应用中,尤其是在神经网络优化问题上,目标函数是一个非凸函数,极值并不是最值,所以可能求出多个极值,不好求。
熵:按照定义来说,凡是和熵有关的大概率是一个凸问题,所以熵的使用对于优化过程来说十分友好。
拉格朗日对偶问题
回到拉格朗日问题
min\ \ f_0(x), x \in \mathbb{R}^n \\
s.t.\begin{cases}
f_i(x)\leq0,\ i=1,2,3,...,m \\
h_i(x)=0,\ i=1,2,3,...,q
\end{cases}
完全等价为:
L(x,\lambda,\upsilon)=f_0(x)+\sum \lambda_if_i(x)+\sum\nu_ih_i(x) \\
\min_x\max_{\lambda,\nu} L(x,\lambda,\nu)\ s.t.\ \lambda\geq0
以上都称为与原问题(验证可以依据 x 是否在可行域讨论)
对偶问题:
g(\lambda,\nu)=\min_x L(x,\lambda,\nu)
\max_{\lambda,\nu}g(\lambda,\nu)=\max_{\lambda,\nu}\min_x L(x,\lambda,\nu)
凸集
凸集定义
\forall x_1,x_2\in C,\ 0<\theta<1 \\
s.t.\ \theta\cdot x_1+(1-\theta)\cdot x_2 \in C
仿射集(一定是凸集)
\forall x_1,x_2\in C,\ \theta\in\mathbb{R} \\
s.t.\ \theta\cdot x_1+(1-\theta)\cdot x_2 \in C
另一种类似线性的仿射集表示(类似,但是仿射不是线性)
这类凸集的交集也是凸集
x,W\in\mathbb{R}^n,b\in\mathbb{R},\ define\ C=\{x|W^T\cdot x+b=0\}
半空间(凸集)
x,W\in\mathbb{R}^n,b\in\mathbb{R},\ define\ C=\{x|W^T\cdot x+b\leq 0\}
半空间的交集也是凸集
对偶问题是凸函数
理解过程:
g(\lambda,\nu)=\min_x L(x,\lambda,\nu)=f_0(x^*)+\sum \lambda_if_i(x^*)+\sum\nu_ih_i(x^*)
其中 x^* 是可行域下拉格朗日函数关于 x 的最小值点,此时 x^* 可视为常数。
目标函数形式:g(\lambda,\nu)=b+W_\lambda\cdot\lambda+W_\nu\cdot\nu
可行域(约束条件):\nu\in\mathbb{R}\ and\ \lambda\geq0
目标函数是凸函数,约束条件是凸集
对偶问题的解和原问题的解
对偶问题的解一定是小于等于原问题的解
简单理解过程,以下不等式恒成立
\max_{\lambda,\nu}L(x,\lambda,\nu)\geq\min_xL(x,\lambda,\nu)
由于
\min_x\max_{\lambda,\nu}L(x,\lambda,\nu)\in\max_{\lambda,\nu}L(x,\lambda,\nu) \\
\max_{\lambda,\nu}\min_xL(x,\lambda,\nu)\in\min_xL(x,\lambda,\nu)
得到
\min_x\max_{\lambda,\nu}L(x,\lambda,\nu)\geq\max_{\lambda,\nu}\min_xL(x,\lambda,\nu)
此时需要解决的问题:寻找某个充分条件,使得
\min_x\max_{\lambda,\nu}L(x,\lambda,\nu)=\max_{\lambda,\nu}\min_xL(x,\lambda,\nu)
即为强对偶关系
先对拉格朗日函数做变形
L(x,\lambda,\upsilon)=f_0(x)+\sum \lambda_if_i(x)+\underline{\sum\nu_ih_i(x)}_{=0} \\
let\begin{cases}
t=f_0(x)\\
u=\vec{f_i(x)} \leq 0 \\
\end{cases} \\
L(x,\lambda,\nu)=t+\lambda^T\cdot u
此时,原问题和对偶问题分别为
original:\ \min_x\{t|(t,u)\in G_1,u\leq0\} \\
G_1=\{(t,u)|x\in D\ (feasible\ region)\} \\
dual:\ \max_\lambda \min_x{\{t+\lambda^T\cdot u|(t,u)\in G_2,\lambda\geq0\}} \\
G_2=\{(t,u)|x\in \mathbb{R}^n\ (all\ region)\} \\
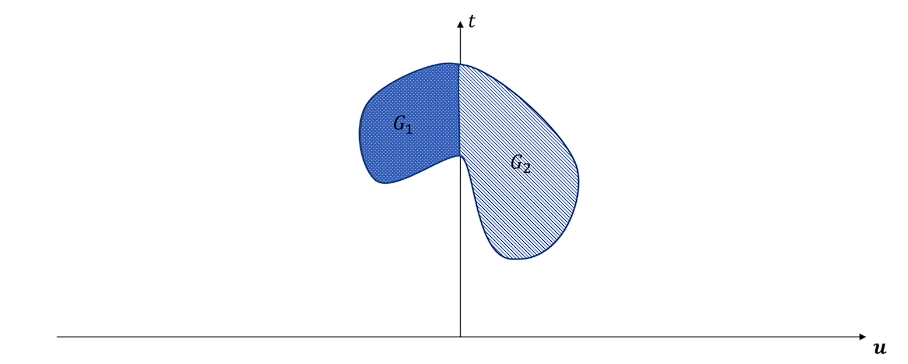
PS: G_2 是 x 全空间下目标函数和约束条件的值域,G_1 是其子集
P^* 为原问题的解,表示在 x 可行域内 t 的最小值,即为 G_1 的下端点。
G^* 为对偶问题的解,按照流程,先调整 x 求出使得直线纵截距最小的点,然后调整斜率 \lambda 使得满足最小值的形况下截距最大。
过程有点抽象,但是简单图示如下
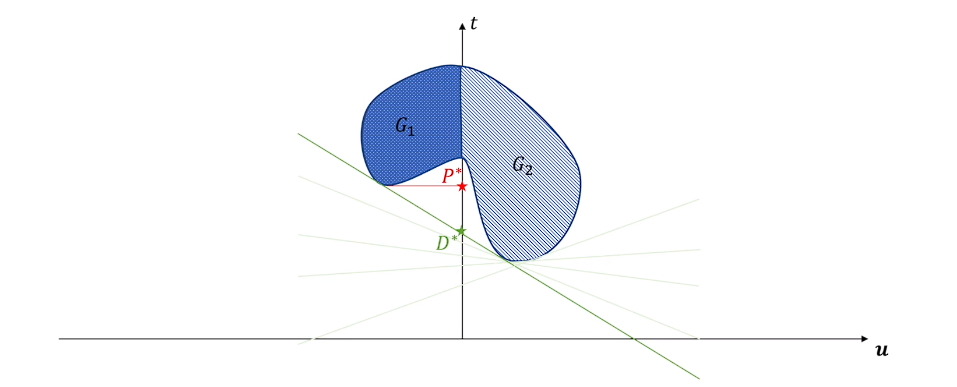
可以看出原问题的解在这个情况下是大于等于对偶问题的解的
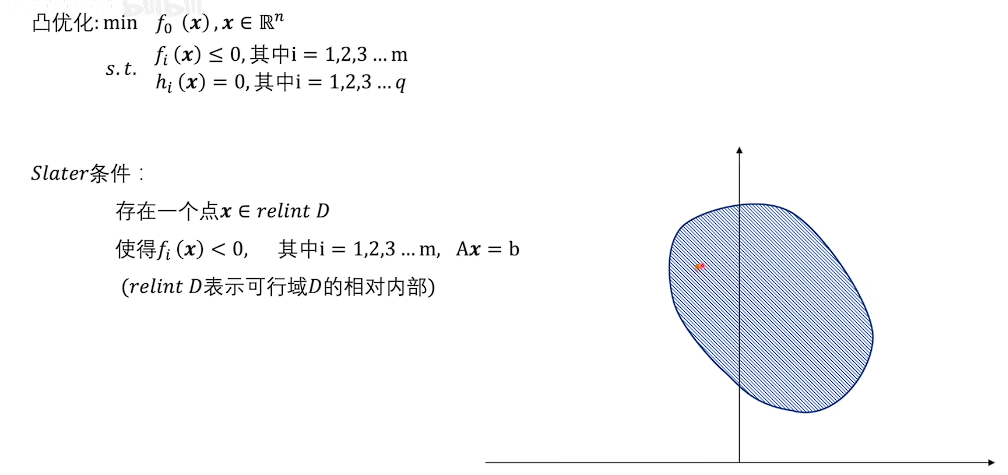
Slater条件
拉格朗日问题强对偶的充分条件
-
原问题是凸问题(目标函数凸函数,可行域是凸集)
-
存在可行域的相对内部的一个点,使得不等式约束非零 f_i(x)<0
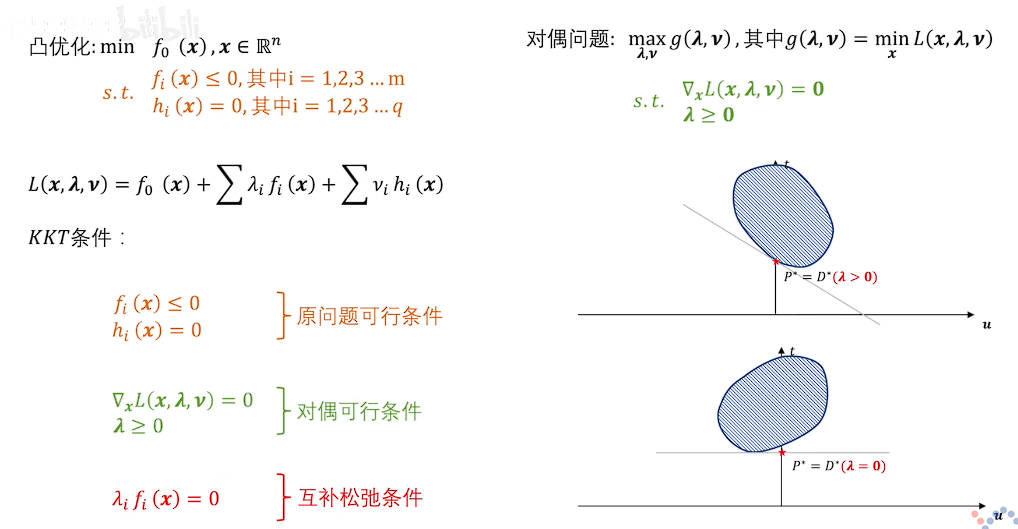
- 原问题可行条件 f_i(x)\leq0,\ h_i(x)=0
- 对偶可行条件 \nabla_xL(x,\lambda,\nu)=0,\ \lambda\geq0
- 互补松弛条件 \lambda_if_i(x)=0
- 值当不等式约束 f_i 紧致时,约束必然取到边界点,此时不等式约束取零 f_i=0 。
- 当不等式约束 f_i 松弛时,拉格朗日乘子 \lambda 取零,消除约束。
扩展
最大熵问题的对偶思想,将超参数调节留到最后

神经网络的损失函数和最大熵的优化问题,损失函数是具有凸形式,但是可行域并非凸域的问题,所以最后神经网络的调节可以看作屏蔽隐藏层带来的非凸影响,在输出层局部形成凸优化问题求解后,再反向传播改变前面结构,不断循环,直到达到一个比较理想的状态。










