深度学习数学基础——概率论|信息论
概率论
大学概率论内容完全够用
信息论
信息熵
定义
Entropy: H(x) = - \sum_{x\in\mathcal{X}}p(x)log\ p(x) = \sum_{x\in\mathcal{X}}p(x)log\ \frac{1}{p(x)}
信息熵和熵没有什么大关系,信息熵可以简单理解为,事件越不可能发生(即所携带的信息)的度量(数学期望)。
H_p(x) = E_{x\in p(x)}\ log\frac{1}{p(x)}
性质
信息熵定义在概率密度函数,信息熵的定义也只依赖于概率分布,本质为数学期望,量度为对数。
tips:
- 0log0 \rightarrow\ 0 .(x\rightarrow 0,\ xlogx \rightarrow\ 0 )
- H(x) only depends on p(x) so we can also write H(p) for H(x)
- When X is uniform over \mathcal{X}, then H(X) = log |\mathcal{X}| 均匀分布最大化离散信息熵
- H_p(X)=log_b a\ H_a(X) 对于不同的度量,只有线性的变化
- 离散随机变量满足 0 \leq H(X) \leq log|\mathcal{X}|
- The logarithm is to the base 2 and the unit is b its. If the base of the logarithm is b, we denote of the entropy by H_p(X). If b = e, the entropy is measured in nats. (奈特)
- Unless otherwise specified, the entropies will be measured in bits.(比特)
伯努利分布为例:
(形式类似于交叉熵损失函数,也就只是类似而已)
H(p)=-plogp-(1-p)log(1-p)
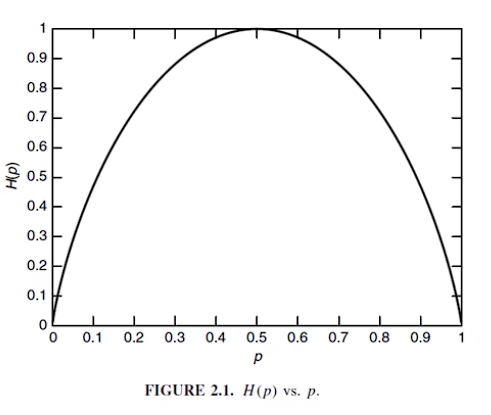
信息熵函数大多数情况下是一个凸函数,所以对信息熵的优化问题往往会优化成为一个凸优化问题。
联合信息熵
类比于联合概率分布,联合信息熵的数学期望形式如下:
H(X,Y) = E_{x,y \ \in\ p(x,y)}log\frac{1}{p(x,y)}
tips
- H(X,X) = H(X)
- H(X,Y)=H(Y,X)
条件熵
已知 P(X|Y) 是一个关于 x,y 的二元概率密度函数,所以条件熵的定义依旧类似
H(Y|X) = E_{x,y\in p(x|y)}log\frac{1}{P(X|Y)}
tips
- H(Y|X)\leq H(Y)
- 计算方法上,很少用定义式而是用如下恒等式(推广到链式法则)
- H(X|Y)+H(Y)=H(Y|X)+H(X)=H(X,Y)
- H(X,Y|Z) = H(X|Z) + H(Y|X,Z) Check p(x,y|z) = p(x|z)p(y|x,z) 贝叶斯公式
- Ven图可以有效理解链式法则
零熵
- 条件熵 H(Y|X)=0, then Y is a function of X 表现为完全不随机的强相关性
- 条件熵(固定值) H(Y|X=x)=0 表示在 X=x 时 Y 只有唯一可能的值 y_0
- 信息熵 H(X)=0 表示概率密度函数为冲击函数,概率分布函数为阶跃函数
KL距离
KL距离是定义在两种不同的概率分布上的一种对两种分布相互之间差异性的度量,不具备范数(metric)的性质。
KL距离只与概率分布有关,计算时共享相同的随机变量
D(p||q) = \sum_{x\in\mathcal{X}}p(x)log\frac{p(x)}{q(x)} = E_p \frac{p(x)}{q(x)}
tips
- 0log\frac{0}{0} = 0,\ 0log\frac{0}{p} = 0,\ plog\frac{p}{0}=\infty
- If there exists x\in\mathcal{X} such that p(x) > 0 and q(x)= 0 ,then D(p||q) = \infty
- D(p||q)\geq0
- D(p||q)=E_p(-log\ q(x))-H(p)
互信息(Mutual Information)
I(X;Y) = D(p(x,y)||p(x)p(y)) = E_{p(x,y)}log\frac{p(x,y)}{p(x)p(y)}
tips
- I(X;Y)=I(Y;X)
- I(X;Y)=0 表示相互独立
- 计算方法:I(X;Y)=H(X)+H(Y)-H(X,Y)
链式法则
H(X_1,X_2,...,X_n)=H(X_1)+H(X_2|X_1)+...+H(X_n|X_1,X_2,...,X_{n-1})
通过条件概率推导而来,Ven图理解更容易
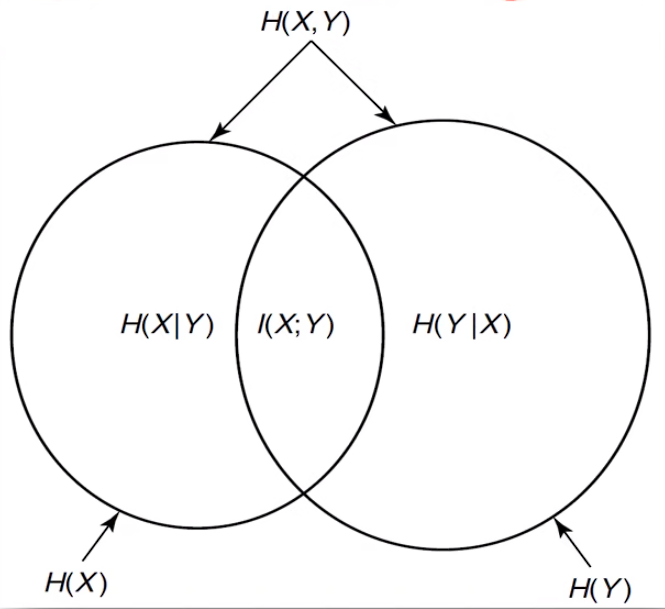
由 H(X_1,X_2) = H(X_2|X_1)+H(X_1) 不难理解链式法则的规律,可以把条件概率看作全概率去除互信息的部分,链式法则就是依次加回来
条件相对熵
本质依旧是两个分布的KL距离
D(q(y|x)||p(y|x))=E_{q(y|x)}log\frac{q(y|x)}{p(y|x)}
tips
计算时依旧是不会使用原定义式,计算用如下等式
D(p(x,y)||q(x,y))=D(p(x)||q(x))+D(p(y|x)||q(y|x))
依旧满足条件熵的链式法则
